2.2 Многомерное распределение

Многоме́рное норма́льное распределение (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения. Случайный вектор, имеющий многомерное нормальное распределение, называется гауссовским вектором

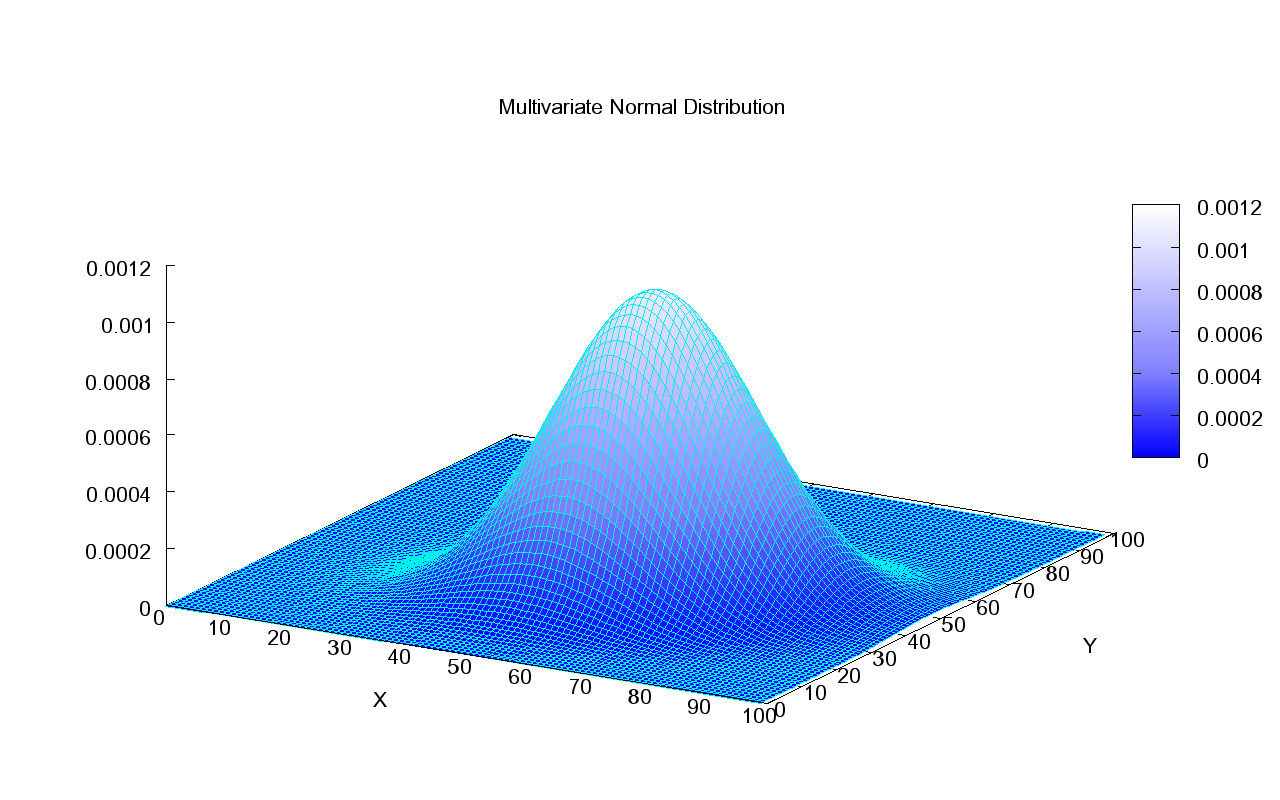
Лучше всего представить процесс построения по шагам. Рассмотрим n независимых случайных величин , имеющих одно и то же (стандартное) гауссовское распределение со средним 0 и стандартным отклонением 1. Эти величины назовем исходными. Каждая величина из исходных величин имеет плотность

$p(x)=\frac{1}{\sqrt{2\pi}}e^{\frac{-x^{2}}{2}}, -\infty<x<\infty$

Определения

Случайный вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n$ имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

• Произвольная линейная комбинация компонентов вектора $\sum\limits_{i=1}^n a_i X_i$ имеет нормальное распределение или является константой.
• Существует вектор независимых стандартных нормальных случайных величин $\mathbf{Z}=(Z_1,\ldots, Z_m)^{\top}$, вещественный вектор $\mathbf{\mu} = (\mu_1,\ldots, \mu_n)^{\top}$ и матрица $\mathbf{A}$ размерности $n \times m$, такие что: $\mathbf{X} = \mathbf{A} \mathbf{Z} + \mathbf{\mu}$.
• Существует вектор $\mathbf{\mu} \in \mathbb{R}^n$ и неотрицательно определённая симметричная матрица $\mathbf{\Sigma}$ размерности $n \times n$, такие что характеристическая функция вектора $\mathbf{X}$ имеет вид:

$\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}}, \mathbf{u} \in \mathbb{R}^n.$ .

Свойства многомерного нормального распределения

Если вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение, то его компоненты $X_i, i=1,\ldots, n$, имеют одномерное нормальное распределение. Обратное, вообще говоря, неверно. Если случайные величины $X_1,\ldots,X_n$ имеют одномерное нормальное распределение и совместно независимы, то случайный вектор $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение. Матрица ковариаций $\Sigma$ такого вектора диагональна. Если $\mathbf{X} = (X_1,\ldots, X_n)^{\top}$ имеет многомерное нормальное распределение, и его компоненты попарно некоррелированы, то они независимы. Однако, если некоторые случайные величины $X_i,\; i = 1 , \ldots$, n имеют одномерные нормальные распределения и попарно не коррелируют, то отсюда не следует, что они независимы и имеют многомерное нормальное распределение. Пример. Пусть $X \sim \mathrm{N}(0,1), а \alpha = \pm 1$ с равными вероятностями. Тогда если $Y = \alpha X \sim \mathrm{N}(0,1)$, то корреляция $X$ и $Y$ равна нулю. Однако, эти случайные величины зависимы и в силу первого утверждения абзаца не имеют многомерного нормального распредедения. Многомерное нормальное распределение устойчиво относительно линейных преобразований. Если $\mathbf{X} \sim \mathrm{N}(\mathbf{\mu},\Sigma)$, а $\mathbf{A}$ — произвольная матрица размерности $m \times n$, то $\mathbf{A}\mathbf{X} \sim \mathrm{N}\left(\mathbf{A}\mathbf{\mu},\mathbf{A}\Sigma \mathbf{A}^{\top}\right)$. Таким преобразованием и сдвигом любое невырожденное нормальное распределение можно привести к вектору независимых стандартных нормальных величин.

Реализация на APL с помошью R

Для начала работы необходимо выполнить синхронизацию APL и R. Это можно выполнить используя инструкцию в открытом доступе на сайте Dyalog.

После этого выполняем следующие действия.

Вычисление определителя

 det←{-/×⌿0 1⌽⍵}

Вычисление гауссиана на сетке точек

 ∇ f←ms gauss x;m;s
[1] m s←ms
[2] f←*-(x-m)+.×(⌹s)+.×,[''](x-m)
[3] f←f÷○2×(det s)*0.5
 ∇

Подготовка данных, диагональная С

 range←{⍵[1]++\0,⍺⍴(|-/⍵)÷⍺}
 y←x←100 range ¯4 4
 xy←x∘.,y
 z←+/¨(⊂(0 0)(2 2⍴1 0 0 1))gauss¨xy
 rinit
 'x'rput x
 'y'rput y
 'z'rput z
 rexec 'persp(x,y,z,theta=30,phi=30,expand=0.5)'

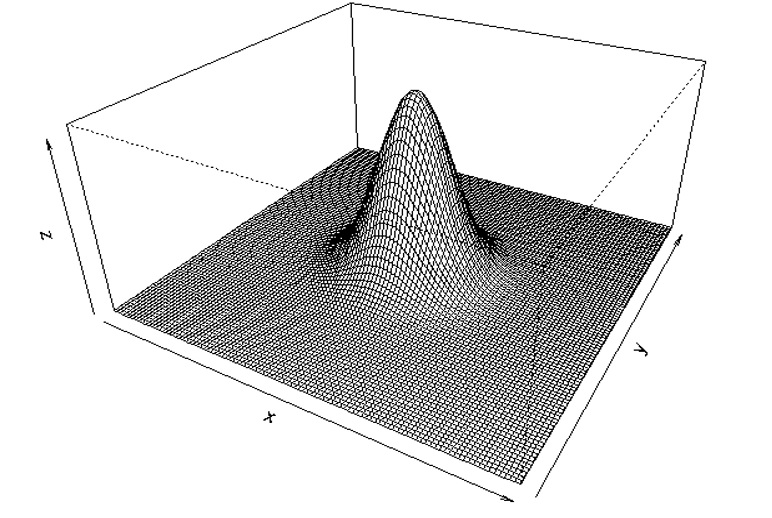
 rexec 'contour(x,y,z)'

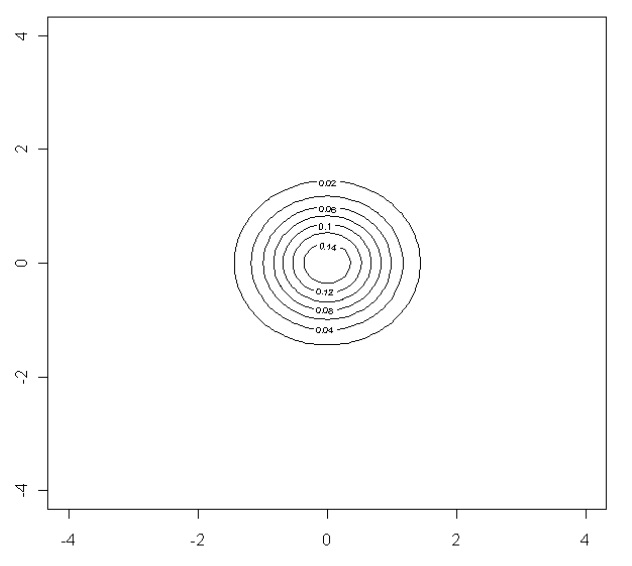
Подготовка данных, ρ=0.9

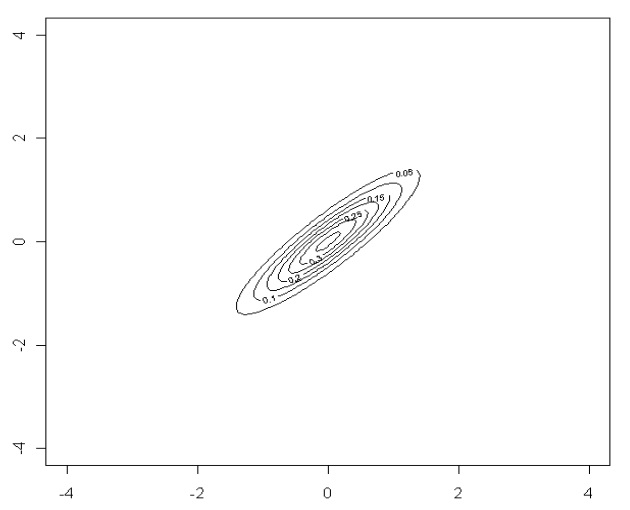
 z←+/¨(⊂(0 0)(2 2⍴1 .9 .9 1))gauss¨xy
 'z'rput z
 rexec 'persp(x,y,z,theta=30,phi=30,expand=0.5)'

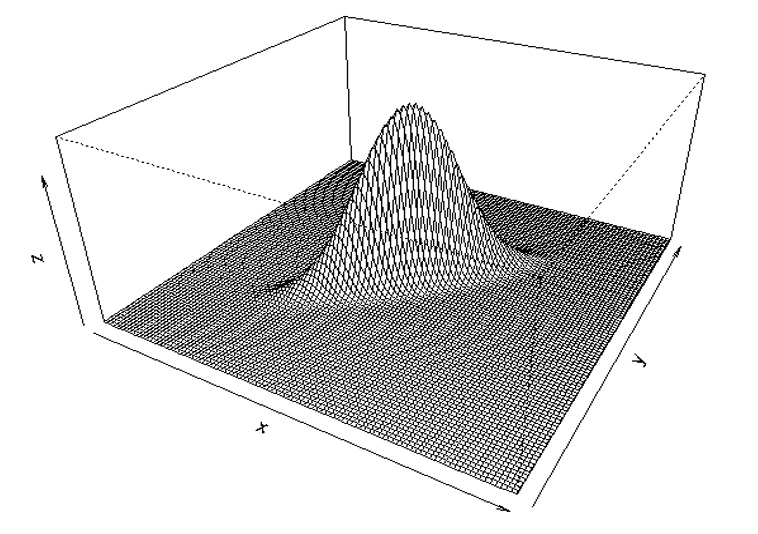
Повернем другой стороной:

 rexec 'persp(x,y,z,theta=-30,phi=30,expand=0.5)'

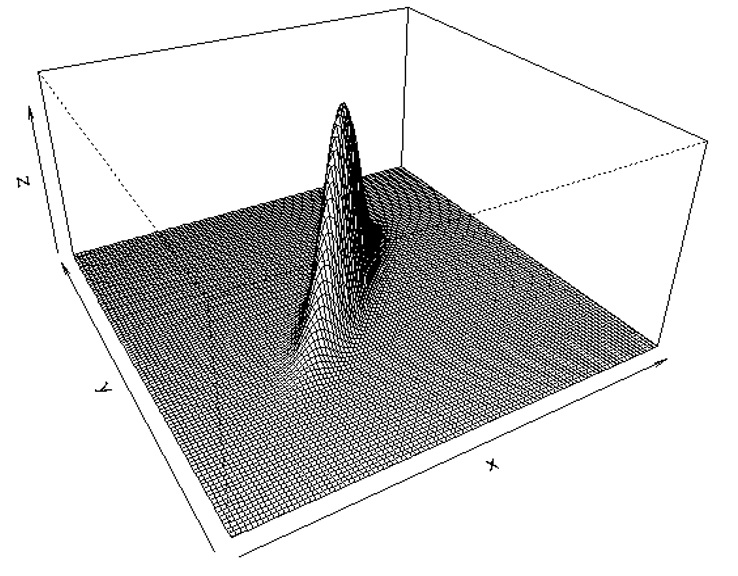
rexec 'contour(x,y,z)'