2.1 Одномерное распределение

Нормальное распределение, также называемое распределением Гаусса¹ — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

$f(x)=\frac{1}{ \sqrt{2\pi\sigma }} e^{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}}$

где параметр $\mu$ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр $\sigma$ среднеквадратическое отклонение ($\sigma^2$ — дисперсия) распределения.

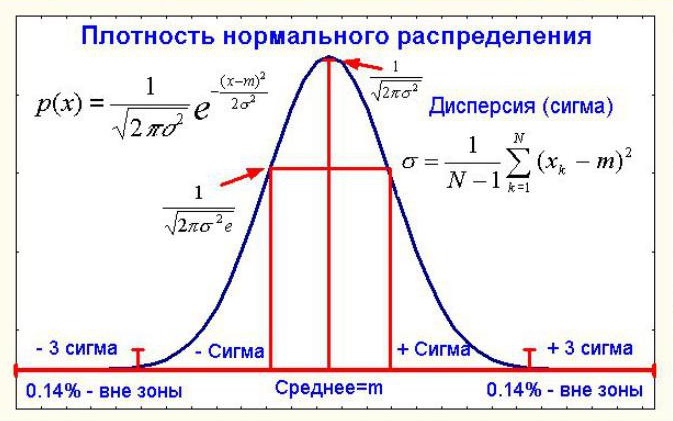
Нормальным распределением является распределение вероятностей (закон, описывающий область значений случайной величины и вероятности их появления), которое задается функцией плотности вероятности, для одномерного случая совпадающей с вышеназванной Гауссовской функцией.

Как видим, одномерное нормальное распределение является двухпараметрическим.

Существует понятие стандартного нормального распределения, когда значение математического ожидания равно нулю ($\mu=0$), а стандартного отклонения – единице ($\sigma=0$).

Значение

Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Гаусс в APL(2d)

Функция должна выглядеть следующим образом:

[0]   f←ms gauss x;m;s
[1]   (m s)←ms
[2]   f←*-((x-m)*2)÷2×s*2
[3]   f←f÷s×(○2)*0.5

Пример:

Вычислим по средним 3.62 и дисперсии 4.12 в точках 3.62 и 5.19

     3.62 4.12 gauss 3.62 5.19
0.09683065058 0.09004928998

Проверка:

     ÷4.12×(○2)*.5
0.09683065058
Верно!

Заметка.

В каких точках оценивать? В любых!

Если хотим построить используем Rang.

Выше приведеный Гаусс не имеет отошение к эксперементальным данным.

Источник Wikipedia.

¹. Иога́нн Карл Фри́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества. ↩