3.1.1 Одномерная кластеризация (Пример из жизни)

Предположим, что нам поступают некие данные, эти данные заполняются в один вектор (в общую кучу) с разных устройств и они получаются при измерении одного физического параметра, но в разных местах.

Условия для правильной класификации, которые предьявляются к датчикам:

они измеряющих один и тот же параметр;
должны быть полностью идентичны;
установлены в одинаковые места в конструкции;
одинаковый режим работы;
одинаковые типы датчиков;
разные объекты контроля;

Что это может быть?

В медицине, к примеру, рентгеновский аппарат. Эти устройства везде идентичны, но объектом контроля являются люди. Другой пример, на реакторах ВВЭР имеется 4 петли в каждой по ГЦНу и на нем измеряется вибрация.

Последний пример рассмотрим по подробней.

Какие данные получатся, если поместить все данные в один файл? И на что они будут похоже?

Идеальный случай.

Четыре одинаково сконструированных ГЦНов, четыре полностью идентичных датчиков, устанленных в одно и тоже место. Можно предположить, что их показания будут практически одинаковыми и если попытаться изобразить их, то это будет выглядить в одномерном случае так как представленно на рисунке 1.

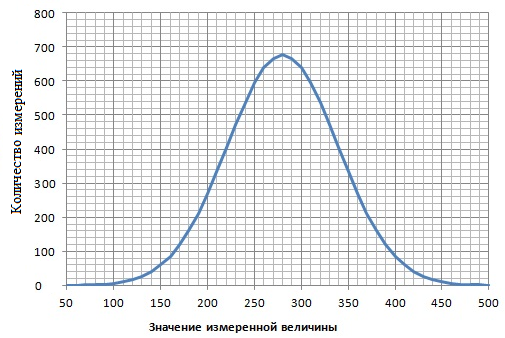
Figure: Рисунок 1 - Данные с 4-х датчиков "в одной куче" (Идиальный случай)

Что дает нам этот график? Что все данные получаемые со всех датчиков практически не отличимы и в плане диагностики такие данные "не интересны". Можно сделать вывод, что всё работает в номенальном режиме без каких либо отклонений от нормальных показателей.

Интересный случай.

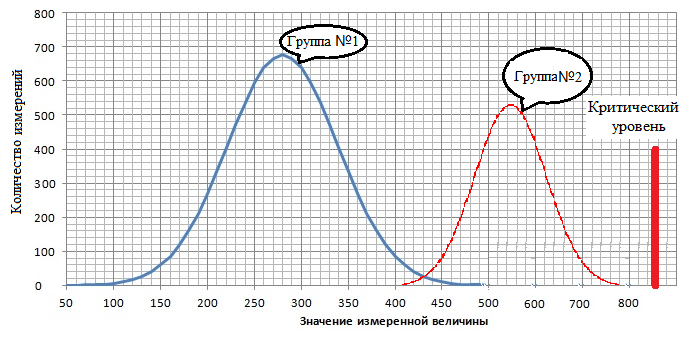
Например, произошло отделение от основных данных какой-то группы значений, как представленно на рисунке 2.

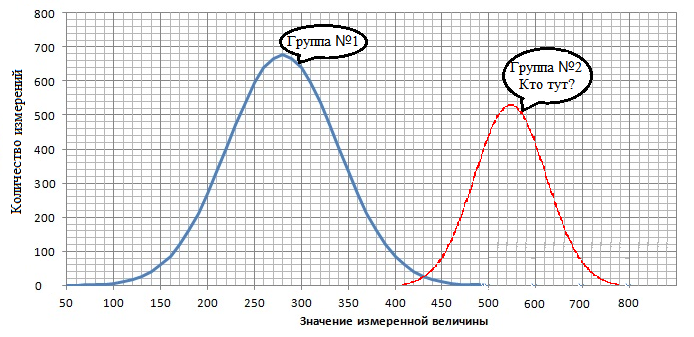
Необходимо определить кто находится в отделившейся области (кто тут?) и когда это сделанно. После проведения такого анализа возможны следующие варианты, что в отделившейся области находятся:

данные с датчиков по всем ГЦНам;
данные с датчика по одному ГЦНу;
данные с датчиков по всем ГЦНам, но преобладающие данные по одному.

Рассмотрим каждый вариант по подробней.

Данные с датчиков по всем ГЦНам

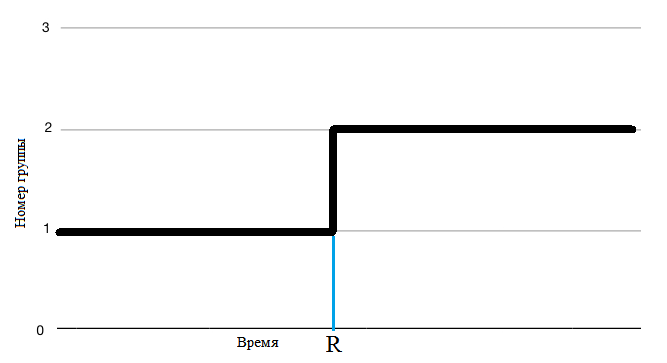
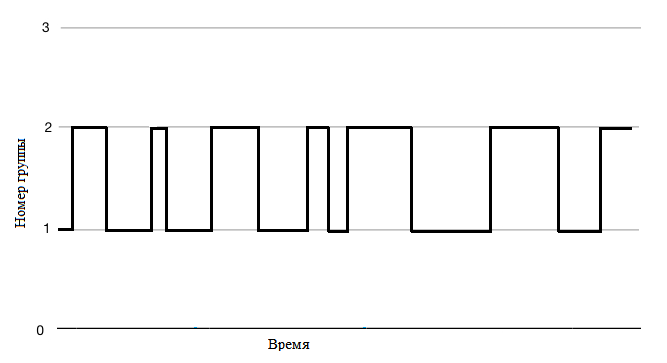
Возможны несколько вариантов: 1) Установка работала в номинальном режиме и в какой-то момент происходит смена режима работы. Тогда построив график номер группы от времени мы увидим изменение группы так, как представленно на рисунке 3.

Figure: Рисунок 3 - Номер группы от времени (Один переход)

2) На установке произошло какое-то изменение на определенный период времени и она поевела себя следующим образом, так как представленно на рисунке 4.

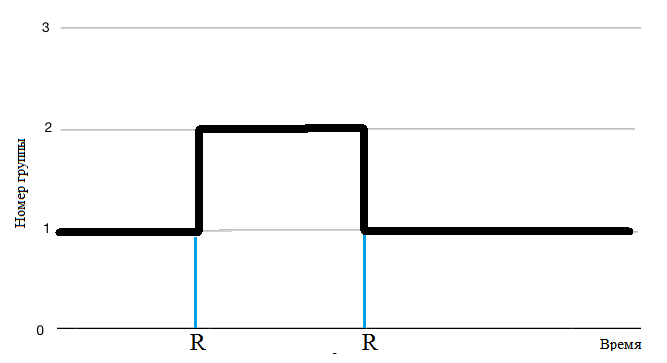
Figure: Рисунок 4 - Номер группы от времени (Два перехода)

По графикам 3 и 4 нас будет интересовать точки R в которых произошло изменение группы. Придется выяснить, что повлияло на это изменеие. Возможно, что эти изменения не вышли за уставки, как показанно на рисунке 5. Но в любом случае нам предстоит выяснить, что это было. Искать информацию в эксплутационных журналах, базах данных, устраивать "допросы" эксплетационному персоналуи операторам и т.д.

Figure: Рисунок 5 - Данные с 4-х датчиков "в одной куче" с границей критического уровня

3) Возможен так же случай, когда происходит изменение данных периодами с быстрой скоростью и хаотично, как показанно на рисунке 6.

Figure: Рисунок 6 - Номер группы от времени (Много переходов)

В таком случае нужно искать параметры которые корелируют с номером группы. Далее думать о физике процессов, искать как они взаимосвязанны.

Данные с датчика по одному ГЦНу

Теоритически установки идентичны, а один ведет себя не как большинство, как показанно на рисунке 7.

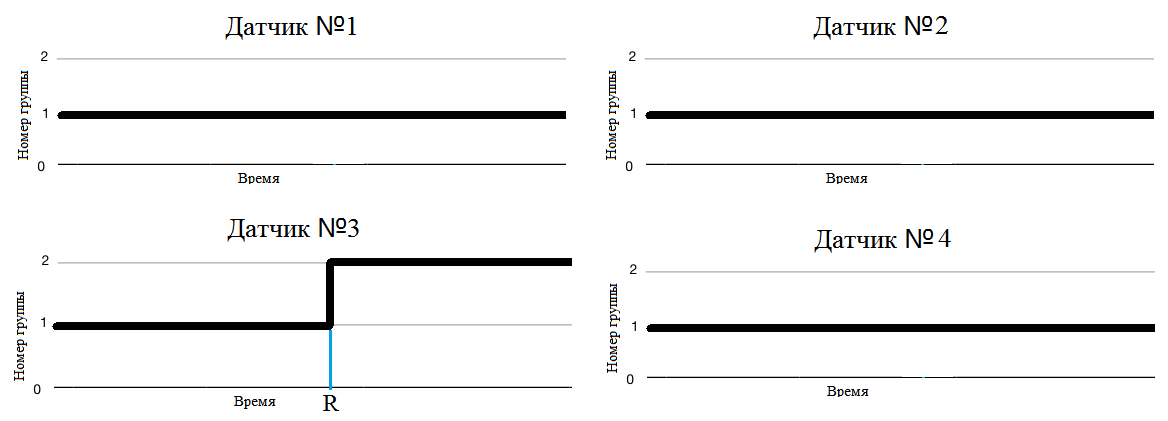
Figure: Рисунок 7 - Данные с каждого датчика (Изменения на датчике №3)

В таком случае можно сделать вывод, что неполадку следует искать именно на этом датчике. Возможно датчик был закреплен не правильно, мог сгореть усилитель, сам датчик не исправен или подключен не правильно. Так же возможно проблема с самой установкой. Следует обратить внимание на, температуры, обороты и т.д., параметр который отличается от параметров на остальных ГЦНах.

Данные с датчиков по всем ГЦНам, но преобладающие данные по одному.

Данная ситуация возможна, если произошло какое-то изменение повлиявщее на все датчики но на один повлияло сильнее и он может преобладать над стальными как показанно на рисунке 8.

Figure: Рисунок 8 - Данные с каждого датчика (Изменения на каждом датчике)

В таком случае нужно искать такой параметр (температуру, давление), который будет коррелировать с тем что мы видим на графике выше.

Пояснение

Сами варианты 1-D, 2-D или N-D:

(1D) Один датчик, один объект контроля. Если мы обнаружим кластеры, то интерпретируем в номера групп от времени. Когда свойств меняющихся во времени не выявленно, то ищим коррелируемые параметры;
(2D) "Один" (однотипный) датчик, разные объекты контроля. Проверяем на то, что проверяли однотипными датчиками;
(ND) "Один" (однотипный) датчик, k штук однотипных объектов контроля.

Интерпритация 1-D

У нас есть данные представленные в таблице №1.

Таблица 1 - данные заданны векторами Х1, Х2 и классом к которому относятся данные в них

X1	X2	Класс
1	1	0
1	0	1
0	1	1
0	0	0

$X1$ и $X2$ наши данные. Чтобы охарактиризовать правило по которому мы сможем без ошибочно определять их класс, придется поразмышлять. Ведь и еденицы и нули, есть в обоих классах. Но здесь достаточно простая задача, достаточно вспомнить правило "Исключающее И" или другими словами, "Сложени по модулю 2".

Возьмём более сложный пример, две группы данных распределённых по гауссовскому закону и имеющие разные средние значения, представленные на рисунке 9.

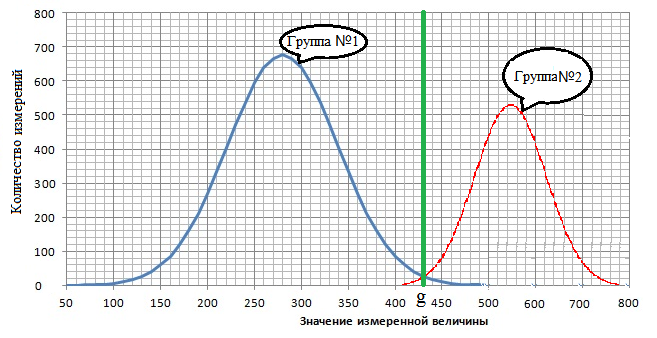
Figure: Рисунок 9 - Данные с 4-х датчиков "в одной куче" с границей разделения (g)

Решающие правило для данного графика - это граница, разделяющая их.

$Правило= \begin{cases} & \text {x < g \implies \omega_{1} } \\ & \text {x > g \implies \omega_{2} } \end{cases}$

Реализуем на APL

Создаём правило генерации рандомных чисел по нормальному распределению:

nrand←{¯6++/?(⍵,12)⍴0}

Подгружаем Rconnect и синхронизируем с RStudio

)copy rconnect
r←⎕new R
 r.init
RConnect initialized

Генерируем 1000 точек:

r.x 'hist(⍵)' (nrand 1000)

Записываем данные:

x←(nrand 5),3+nrand 7
c←5 7/1 2

Генерируем пороги:

 g←.5×2+/x[⍋x]

Создаем проверку на ошибки и проверяем их количество:

⎕vr'errors'
 ∇ e←g errors x;c
[1] x c←x
[2] e←+/(x<g)∧c=2
[3] e←e,+/(x>g)∧c=1
 ∇ 

e←g errors¨ ⊂x c

Смотрим количество ошибок (первая цифра) и на каком месте минимум (вторая цифра):

{⍵⍳⎕←⌊/⍵}+/¨e
0
5

Смотри его значение:

g[5]
0.8298365211

Строим график количества ошибок от уровня порога (Рисунок 10).

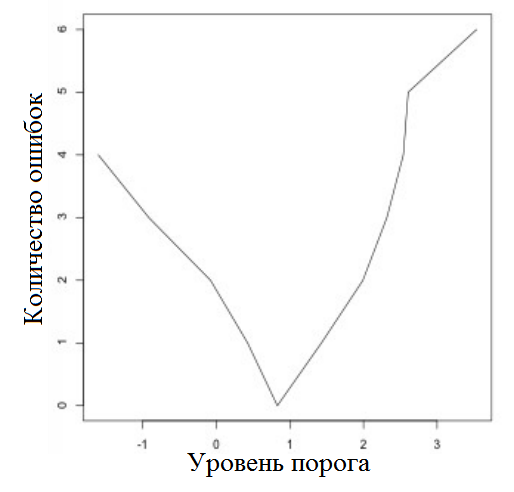
Figure: Рисунок 10 - Количество ошибок от уровня порога

Применение к своим вариантам.

Пример варианта данных в таблице 2.

Таблица 2 - данные заданны векторами Х1, Х2 и классом к которому относятся данные в них

X1
1.3 1.9 3 4.9 4.4 4.4 1.5 4.7 4.1 1.5 1.6 4.8 1.4 1.7 1.2 1.3 1.5 4 4.4 1.4 4.7 4.5 1.5 1.4 1.6 1.5 4.2 1.3 4.6 4.9

У нас есть один столбец $X1$ , он может выглядить двумя способама, как показанно на рисунке 11.

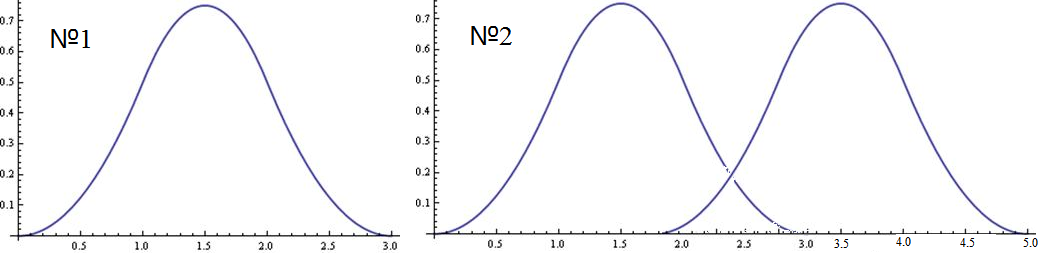
Figure: Рисунок 11 - №1 - все данные в одной группе, №2 - данные разделились на две группы

Чтобы понять это, строим по имеющимся данным стебель с листьями для наглядности.

Как видно из построения на рисунке 12 получается два класса и еще одна точка лежащая почти на равном удаление от обоих классов (между ними). Условно назовем их класс 1 и класс 2.

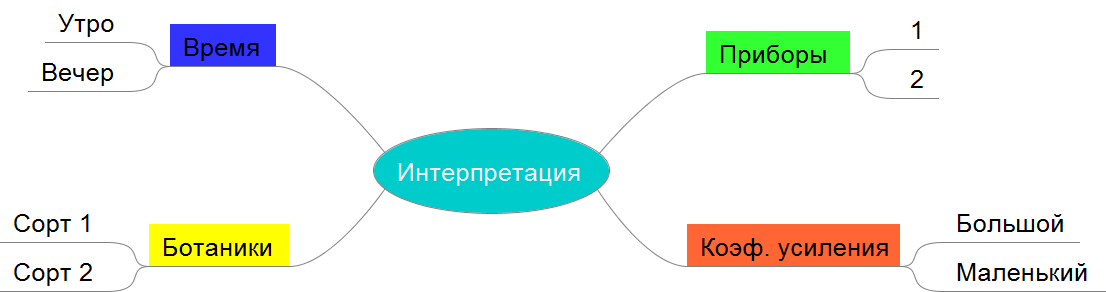
Затем были даны номера классов [1] [2], представлены на рисунке 13.

При сопоставлении данных и номеров классов можно увидеть, что номер класса соответствует той или иной группе которые получились при построении стебля с листьями.

Рисунок 12 - Стебель с листьями по нашим данным Рисунок 13 - Номер класса и наши данные

Интерпретировать можно по разному получившиеся группы, типы и т.д.. Разные приборы использовались при измерении или разные коэф. усиления, а так же возможно разные сорта одного и того же растения. Пример представлен на рисунке 14.

Figure: Рисунок 14 - Пример интерпретации

Интерпритация 2-D

Построение выполняем по двум признакам в Rstudio.

Записываем данные в программу.

h1=c(1.3,1.9,3,4.9,4.4,4.4,1.5,4.7,4.1,1.5,1.6,4.8,1.4,1.7,1.2,1.3,1.5,4,4.4,
1.4,4.7,4.5,1.5,1.4,1.6,1.5,4.2,1.3,4.6,4.9)
h2=c(0.2,0.2,1.1,1.4,0.2,1.4,1.4,0.2,1.4,1.3,0.2,0.6,1.4,0.2,0.5,0.2,0.4,0.2,
1.3,1.2,0.3,1.4,1.5,0.4,0.2,0.4,0.1,1.3,0.2,1.4,1.5)

Стороим график и результат видим на рисунке 15.

plot(h1,h2)

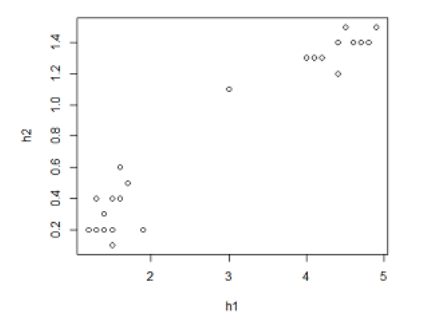
Figure: Рисунок 15 - График построения наших данных

На графике, построенном по двум признакам отчетливо видны два кластера(скопления точек).

5.3 Кластерный анализ 3-D

Для примеров Кластерного анализа 3-D мы будем использовать встроенные в R данные iris. Это данные заимствованны из работы знаменитого математика (и биолога) Р. Фишера¹. Они описывают разнообразие нескольких признаков трёх видов ирисов (многолетние корневищные растения, относящиеся к семейству Ка- сатиковых или Ирисовых). Эти данные состоят из 5 переменных (колонок), при- чём последняя колонка — это название вида.

А теперь визуализируем четыре из пяти колонок iris при помощи пакета RGL:

> library(rgl)
> cc<-c(rep(1,50), rep(2,50), rep(3,50))
> # сс делаем для того что бы кластеры окрасились в нужный им цвета
> plot3d(iris$Sepal.Length, iris$Sepal.Width, iris$Petal.Length, col=cc, size=3)

Когда мы визуализировали наши данные мы можем начать анализ!

Нужно помнить и понимать важную последовательность действий при кластерном анализе

КЛАСТЕРНЫЙ АНАЛИЗ ---> ИНТЕРПРЕТАЦИЯ

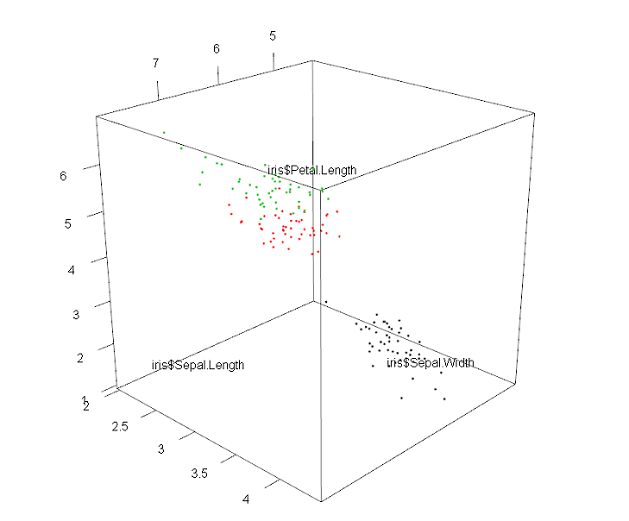
Из получившейся визуализации наших данных можно произвести интерпретацию следующим образом:

Сорт 1 (окрашен в черный цвет);
Смесь 2-х сортов (окрашены в зеленый и красный цвет).

Соответственно видим, что получается 3 кластера по 3-м сортам одного растения.