4.3 LINEAR REGRESSION
R Анализ данных Примеры:
Рассмотрим всё выше сказанное на простых примерах линейной регресси на языке R используя функцию lmrob в пакете robustbase.
Данная функция (lmrob) является оценщиком ММ-типа линейной регрессии.
Робастная регрессия является альтернативой регрессии по методу наименьших квадратов, когда данные загрязнены выбросам с наиболее значимыми наблюдениями, которые можно использовать с целью выявления наиболее значимых наблюдений.
Далее будут использоваться следующие пакеты. Убедитесь, что вы можете загрузить их, прежде чем пытаться запустить примеры приведённые ниже. Если вы не имеете установленного пакета, выполните команду: install.packages ( "имя_пакета"), или если вы видите, что версия устарела, выполните следующую команду: update.packages ().
require (foreign) require (MASS)
require быстро выполнит проверку наличия пакета. Если указанного пакета не будет обнаруженно, то она подгрузит и активирует его, если пакет уже загружен, то она просто включет его.
Информация о версии: Код для для дальнейших вычислений в данной главе был протестирован в R версии 3.1.1 (2016-03-13)
With: MASS 7.3-33; foreign 0.8-61; knitr 1.6; boot 1.3-11; ggplot2 1.0.0; dplyr 0.2; nlme 3.1-117
Обратите внимание: Цель данной главы, показать, как использовать различные команды анализа данных. Она не охватывает все аспекты процесса исследования, которые специалист по анализу должен проделывать. В частности, она не распространяется на очистку данных и проверки, проверки предположений, модель диагностики или потенциальных последующих анализов.
Введение
Давайте начнем наше обсуждение на робастной регрессии с некоторыми терминами в линейной регрессии.
Residual: Разница между предсказанным значением (на основе уравнения регрессии) и фактическим, наблюдаемым.
Outlier: В линейной регрессии, выбросами является наблюдение с большим остатком. Другими словами, это наблюдение которого зависит от переменной чьё значение является необычным, учитывая его значение на предикторе. Выброс может указывать на образец особенности или может указывать на ошибку ввода данных или другие проблемы.
Leverage: наблюдение с экстремальным значением переменной предсказания, является точкой с высоким плечом. Плечо является мерой того, насколько независимая переменная отклоняется от своего среднего значения. Точки высокого плеча может оказать большой эффект на оценку коэффициентов регрессии.
Influence: наблюдение называется влиятельным, если удаление наблюдения существенно изменяет оценку коэффициентов регрессии. Влияние можно рассматривать как произведение рычагов и выбросов.
Cook's distance (or Cook's D): Мера, которая сочетает в себе информацию рычагов и остатков наблюдения.
Робастная регрессия может быть использована в любой ситуации, в которой вы будете использовать регрессии методом наименьших квадратов. При установке регрессии наименьших квадратов, мы могли бы найти какие-то выбросы и высокие отклонения точек от основных данных. Мы решили, что эти точки данных не являются ошибками при вводе данных, но они от другой области, чем большинство наших данных. Таким образом, у нас нет никаких убедительных оснований исключать их из анализа. Робастная регрессия может быть хорошей стратегией, поскольку она представляет собой компромисс между исключением этих точек полностью из анализа, включая все точки данных и обработки всех их в равной степени МНК регрессии. Идея робастной регрессии является взвешивание наблюдений по разному в зависимости от того, насколько "хороши" эти наблюдения. Грубо говоря, это форма взвешенной и повторяющейся регрессии наименьших квадратов.
Команда rlm в MASS пакет реализует несколько версий надежной регрессии. В этой главе мы покажем M-оценку с Huber и bisquare взвешивания. Эти два очень стандартные функции. М-оценка определяет весовую функцию таким образом, чтобы оценить уравнение становится . Но весовые коэффициенты зависят от остатков и остатков на весах. Уравнение решается с помощью "Iteratively Reweighted Least Squares" - Итеративно взвешенный метод наименьших квадратов (IRLS). Например, матрица коэффициентов при итерационном j является , где индексы указывают на матрицу на конкретной итерации (not строку или столбец). Процесс продолжается до тех пор, пока они не сходятся. В Huber взвешиванием, наблюдения с маленькими остатками получить вес 1, и чем больше остаток, тем меньше вес. Это определяется весовой функцией
С bisquare взвешивания, все случаи с ненулевым остатком, получить взвешенные по крайней мере мало.
Описание примера данных
Для нашего анализа данных ниже, мы будем использовать набор данных преступлений, которые появляются в Statistical Methods for Social Sciences, Third Edition by Alan Agresti and Barbara Finlay (Prentice Hall, 1997). Переменные состояния id ( sid ), название штата ( state ), насильственные преступления на 100000 человек ( crime ), убийства в 1,000,000 ( murder ), процент населения, проживающего в городских районах ( pctmetro ), процент населения, белых ( pctwhite ), процент населения с средним образованием или выше ( pcths ), процент населения, живущего за чертой бедности ( poverty ), и процент населения, которые являются родители - одиночки ( single ). Он имеет 51 наблюдение. Мы будем использовать poverty и single для прогнозирования crime (преступности).
cdata <- read.dta("http://www.ats.ucla.edu/stat/data/crime.dta") summary(cdata)
## sid state crime murder
## Min. : 1.0 Length:51 Min. : 82 Min. : 1.60
## 1st Qu.:13.5 Class :character 1st Qu.: 326 1st Qu.: 3.90
## Median :26.0 Mode :character Median : 515 Median : 6.80
## Mean :26.0 Mean : 613 Mean : 8.73
## 3rd Qu.:38.5 3rd Qu.: 773 3rd Qu.:10.35
## Max. :51.0 Max. :2922 Max. :78.50
## pctmetro pctwhite pcths poverty
## Min. : 24.0 Min. :31.8 Min. :64.3 Min. : 8.0
## 1st Qu.: 49.5 1st Qu.:79.3 1st Qu.:73.5 1st Qu.:10.7
## Median : 69.8 Median :87.6 Median :76.7 Median :13.1
## Mean : 67.4 Mean :84.1 Mean :76.2 Mean :14.3
## 3rd Qu.: 84.0 3rd Qu.:92.6 3rd Qu.:80.1 3rd Qu.:17.4
## Max. :100.0 Max. :98.5 Max. :86.6 Max. :26.4
## single
## Min. : 8.4
## 1st Qu.:10.1
## Median :10.9
## Mean :11.3
## 3rd Qu.:12.1
## Max. :22.1
Использование робастного регрессионного анализа
В большинстве случаев мы начинаем, запустив регрессию МНК и делаем некоторую диагностику. Начнем с того, что запустим регрессию МНК и глядя на диагностические участки, исследуем остатки, подобранными значениями, расстояния Кука и рычагов.
summary(ols <- lm(crime ~ poverty + single, data = cdata))
## Call:
## lm(formula = crime ~ poverty + single, data = cdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -811.1 -114.3 -22.4 121.9 689.8
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1368.19 187.21 -7.31 2.5e-09 ***
## poverty 6.79 8.99 0.76 0.45
## single 166.37 19.42 8.57 3.1e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 244 on 48 degrees of freedom
## Multiple R-squared: 0.707, Adjusted R-squared: 0.695
## F-statistic: 58 on 2 and 48 DF, p-value: 1.58e-13
opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(ols, las = 1)

par(opar)
Из этих графиков, можно выделить наблюдения 9, 25 и, возможно, 51-ое проблемные в нашей модели. Мы можем посмотреть на эти наблюдения, чтобы увидеть, что они из себя представляют.
cdata[c(9, 25, 51), 1:2]
## sid state
## 9 9 fl
## 25 25 ms
## 51 51 dc
DC, Флорида и Миссисипи имеют либо высокое плечо или крупные остатки. Мы можем отобразить наблюдения, которые имеют относительно большие значения Cook's D. Обычная точка отсечки , где n есть число наблюдений в наборе данных. Мы будем использовать этот критерий для выбора значения для отображения.
d1 <- cooks.distance(ols)
r <- stdres(ols)
a <- cbind(cdata, d1, r)
a[d1 > 4/51, ]
## sid state crime murder pctmetro pctwhite pcths poverty single d1
## 1 1 ak 761 9.0 41.8 75.2 86.6 9.1 14.3 0.1255
## 9 9 fl 1206 8.9 93.0 83.5 74.4 17.8 10.6 0.1426
## 25 25 ms 434 13.5 30.7 63.3 64.3 24.7 14.7 0.6139
## 51 51 dc 2922 78.5 100.0 31.8 73.1 26.4 22.1 2.6363
## r
## 1 -1.397
## 9 2.903
## 25 -3.563
## 51 2.616
Вероятно, мы должны опустить DC, чтобы начать анализ, так как это даже не штат. Мы включаем ее в анализ, чтобы показать, что она имеет большой Cook's D и продемонстрируем, как она будет обрабатываться rlm. Теперь мы будем смотреть на остатки. Мы будем генерировать новую переменную с именем absr1, в которой будут абсолютные значения остатков (поскольку знак остатка не имеет значения). Затем мы напечатаем десять наблюдений с самыми высокими абсолютными весами остатков.
rabs <- abs(r)
a <- cbind(cdata, d1, r, rabs)
asorted <- a[order(-rabs), ]
asorted[1:10, ]
## sid state crime murder pctmetro pctwhite pcths poverty single d1
## 25 25 ms 434 13.5 30.7 63.3 64.3 24.7 14.7 0.61387
## 9 9 fl 1206 8.9 93.0 83.5 74.4 17.8 10.6 0.14259
## 51 51 dc 2922 78.5 100.0 31.8 73.1 26.4 22.1 2.63625
## 46 46 vt 114 3.6 27.0 98.4 80.8 10.0 11.0 0.04272
## 26 26 mt 178 3.0 24.0 92.6 81.0 14.9 10.8 0.01676
## 21 21 me 126 1.6 35.7 98.5 78.8 10.7 10.6 0.02233
## 1 1 ak 761 9.0 41.8 75.2 86.6 9.1 14.3 0.12548
## 31 31 nj 627 5.3 100.0 80.8 76.7 10.9 9.6 0.02229
## 14 14 il 960 11.4 84.0 81.0 76.2 13.6 11.5 0.01266
## 20 20 md 998 12.7 92.8 68.9 78.4 9.7 12.0 0.03570
## r rabs
## 25 -3.563 3.563
## 9 2.903 2.903
## 51 2.616 2.616
## 46 -1.742 1.742
## 26 -1.461 1.461
## 21 -1.427 1.427
## 1 -1.397 1.397
## 31 1.354 1.354
## 14 1.338 1.338
## 20 1.287 1.287
Теперь давайте запустим нашу первую робастную регрессию. Робастная регрессия осуществляется путем итерированными повторно метода взвешенных наименьших квадратов (IRLS). Команда для запуска робастной регрессии является rlm в MASS пакете. Есть несколько весовые функции, которые могут быть использованы для IRLS. Мы будем сначала использовать весовые коэффициенты Huber в данном примере. Затем мы будем смотреть на конечные веса, созданных в процессе IRLS. Это может быть очень полезным.
summary(rr.huber <- rlm(crime ~ poverty + single, data = cdata))
## Call: rlm(formula = crime ~ poverty + single, data = cdata)
## Residuals:
## Min 1Q Median 3Q Max
## -846.1 -125.8 -16.5 119.2 679.9
##
## Coefficients:
## Value Std. Error t value
## (Intercept) -1423.037 167.590 -8.491
## poverty 8.868 8.047 1.102
## single 168.986 17.388 9.719
##
## Residual standard error: 182 on 48 degrees of freedom
hweights <- data.frame(state = cdata$state, resid = rr.huber$resid, weight = rr.huber$w)
hweights2 <- hweights[order(rr.huber$w), ]
hweights2[1:15, ]
## state resid weight
## 25 ms -846.09 0.2890
## 9 fl 679.94 0.3595
## 46 vt -410.48 0.5956
## 51 dc 376.34 0.6494
## 26 mt -356.14 0.6865
## 21 me -337.10 0.7252
## 31 nj 331.12 0.7384
## 14 il 319.10 0.7661
## 1 ak -313.16 0.7807
## 20 md 307.19 0.7958
## 19 ma 291.21 0.8395
## 18 la -266.96 0.9159
## 2 al 105.40 1.0000
## 3 ar 30.54 1.0000
## 4 az -43.25 1.0000
Мы можем видеть, что грубо говоря, как абсолютная остаточность идет вниз, вес идет вверх. Другими словами, в случаи с большим остаткам, как правило, вниз-взвешенный. Этот вывод показывает нам, что наблюдение за Миссисипи будет вниз-взвешенна больше всего. Флорида также будет существенно вниз-взвешенна. Все наблюдения не показанные выше, имеют вес 1. В МНК регрессии, во всех случаях имеют вес 1. Следовательно, чем больше случаев в робастной регрессии, которые имеют вес, близкий к одному, тем ближе результаты МНК и робастной регрессий.
Далее, давайте выполним ту же модель, но с использованием bisquare весовой функции. Опять же, мы можем посмотреть на веса.
rr.bisquare <- rlm(crime ~ poverty + single, data=cdata, psi = psi.bisquare)
summary(rr.bisquare)
##
## Call: rlm(formula = crime ~ poverty + single, data = cdata, psi = psi.bisquare)
## Residuals:
## Min 1Q Median 3Q Max
## -906 -141 -15 115 668
##
## Coefficients:
## Value Std. Error t value
## (Intercept) -1535.334 164.506 -9.333
## poverty 11.690 7.899 1.480
## single 175.930 17.068 10.308
##
## Residual standard error: 202 on 48 degrees of freedom
biweights <- data.frame(state = cdata$state, resid = rr.bisquare$resid, weight = rr.bisquare$w)
biweights2 <- biweights[order(rr.bisquare$w), ]
biweights2[1:15, ]
## state resid weight
## 25 ms -905.6 0.007653
## 9 fl 668.4 0.252871
## 46 vt -402.8 0.671495
## 26 mt -360.9 0.731137
## 31 nj 346.0 0.751348
## 18 la -332.7 0.768938
## 21 me -328.6 0.774103
## 1 ak -325.9 0.777662
## 14 il 313.1 0.793659
## 20 md 308.8 0.799066
## 19 ma 297.6 0.812597
## 51 dc 260.6 0.854442
## 50 wy -234.2 0.881661
## 5 ca 201.4 0.911714
## 10 ga -186.6 0.924033
Мы можем видеть, что вес, придаваемый Миссисипи значительно ниже, используя bisquare весовой функции, чем весовой функции Huber и оценки параметров из этих двух различных методов взвешивания различаются. При сравнении результатов регулярной МНК регрессии и робастной регрессии, эти результаты очень разные, вы, скорее всего хотите использовать результаты от робастной регрессии. Большие различия позволяют предположить, что параметры модели в настоящее время под сильным влиянием выбросов. Различные функции имеют свои преимущества и недостатки. Веса Huber могут испытывать трудности с серьезными выбросами и bisquare веса могут иметь трудности, схождения или может дать несколько решений.
Как вы можете видеть, результаты двух анализов достаточно разные, особенно в отношении коэффициента single и константы ( intercept ). В то время как обычно мы не заинтересованы в постоянной, если вы сосредоточилось на одином или обойх предикторах, константа была бы полезной. С другой стороны, можно заметить, что бедность не является статистически значимым в любом анализе, в то время как single имеет большое значение в обоих анализах.
Вывод: Примеры, показанные выше представили R код для оценки M. Есть и другие варианты оценки имеющихся в rlm и другие команды R и пакеты: Наименее отдаленные квадраты с использованием ltsReg в robustbase пакете и MM с помощью rlm.
Который мы сейчас и рассмотрим.
Множественная модель линейной регрессии предполагает, что в добавление к независимым переменных кроме того и переменная измеряется, что может быть объяснено с помощью линейной комбинации переменных. Точнее, модель говорит, что для всех наблюдений (, ) он считает, что ,
где ошибки они считаются независимыми и одинаково распределены с нулевым средним и постоянной дисперсией . Применение оценки регрессии к данным дает коэффициент регрессии, в сочетании, как . Остаток в данном случае определен как разность между наблюдаемой реакцией и его оценочного значения .
Классические методом наименьших квадратов (LS) метод оценки минимизирует сумму квадратов остатков. Он пользуется популярностью, потому что позволяет вычислять оценки регрессии в явном виде, и это является оптимальным, если ошибки нормально распределены. Тем не менее, LS является чрезвычайно чувствительным к регрессионным выбросам, то есть наблюдениями, которые не подчиняются линейной структуре, образованное большинством данных.
Оценка наименьших квадратов (ОНК) предложил Roussee следующее
где упорядоченное среднеквадратичное отклонение. (Сначала они возводятся в квадрат и затем упорядочивает) Значение играет ту же роль, что и в оценке МНК. Для , мы получаем разбиение значений на 50%, в то время как для больших , мы получаем примерно . Быстрый алгоритм для оценки ОНК(БЫСТРАЯ-ОНК) был развит.
Масштаб ошибки можно оценить так:
где является остатком от подгонки ОНК и является константой, что делает несмещенная при гауссовском распределении ошибок. Затем мы можем определить регрессию выбросов по их стандартизированной ОНК остатки . Мы также можем использовать стандартную ОНК остатков, назначив вес каждого наблюдения. Взвешенная оценка НК с этими весами ОНК получает хорошие устойчивые свойства ОНК, но является более эффективным и дает обычную выводноную величину, такие как t-статистика, F-статистике, статистики и соответствующие -значения.
Карта выбросов на участках стандартизированной ОНК остатки против устойчивых расстояний на основе (для примера) оценщика МНК, который применяется к -переменным. Это позволяет различать вертикальные выбросы (с небольшими расстояниями надежных и отдалённых выбросов), хорошие рычаги точек (с отдалёнными надежными расстояниями, но небольшие выбросы), а также плохие рычаги точек (с окраин надежных расстояний и отдалённые выбросы).
Самая ранняя теория надежной регрессии на основе М-оценок, R-оценки и L-оценки. Разброс значений всех этих методов это 0% из-за их уязвимости к плохим точкам рычагов. Обобщенные M-оценки (GM-оценки) были первыми, чтоб достигали положительного разброса значений, которое, к сожалению, до сих пор опускались к нулю при увеличении р.
Низкая эффективность конечно образеца ОНК может быть улучшена путем замены его целевой функции с помощью более эффективно применения к выбросам шкалы оценки. Такой подход привел к введению регрессии S-оценки и ММ-оценки.
Описание функции
Разберём по подробнее функцию lmrob. В неё входит следующие:
lmrob(formula, data, subset, weights, na.action, method = "MM",
model = TRUE, x = !control$compute.rd, y = FALSE,
singular.ok = TRUE, contrasts = NULL, offset = NULL,
control = NULL, init = NULL, ...)
formula - символическое описание модели, в правильной форме;
data - (данные) дополнительный набор данных, список или окружающая среда (или объект сжимаемый с помощью as.data.frame на набор данных), содержащий переменные значения в модели. Если не найден в данных, переменные берутся из окружения (формула), как правило, в среду, котора называется lmrob;
subset - (подмножество) дополнительный вектор, определяющий набор наблюдений, которые будут использоваться в процессе подгонки;
weights - (веса) дополнительный вектор весов, который будет использоваться в процессе подгонки (в дополнение к робастности весов, вычисленных в процессе подгонки);
na.action - функция, которая указывает на то, что должно произойти, когда данные содержат N/a's. По умолчанию устанавливается настройкой na.action опции, и na.fail, если это не устраивает. "factory-fresh" по умолчанию na.omit. Другой возможный значение равно NULL, в этом случае никаких действий не будет;
method = "MM" - строка, определяющая оценщика цепи. ММ интерпретируется как (См. Детали, в частности, рекомендуемую в данный момент параметр = "KS2014");
model = TRUE, x = !control$compute.rd, y = FALSE - логические выражения. Если TRUE соответствующие компоненты подгонки (модель frame, матричные модели, ответ) возвращаются;
singular.ok = TRUE - если FALSE (по умолчанию в S, но не в R) особой подгонки является ошибкой;
contrasts = NULL - (контрасты) дополнительный список. Смотрите contrasts.arg из model.matrix.default;
offset = NULL - (смещение) это может быть использовано для определенияаприорных известных компонент для включения в линейное предсказание во время примера. offset может быть включен в формулу вместо или сам по себе, и если указаны оба (данные и offset) используют их сумма;
control = NULL список с указанием параметров управления, используйте функцию lmrob.control (.) и увидете страницу справки;
init = NULL - необязательный аргумент, чтобы указать или поставить первоначальную оценку;
... - дополнительные аргументы могут быть использованы для определения параметров управления непосредственно вместо (а не в дополнение к!) параметра контроля.
Работа функции
Фиксируем значение seed для воспроизводимости результатов.
set.seed(0)
Подгружаем данные.
data(starsCYG, package = "robustbase")
Строим данные.
plot(starsCYG)
Вычисляем регрессии.
lmST <- lm(log.light ~ log.Te, data = starsCYG) (RlmST <- lmrob(log.light ~ log.Te, data = starsCYG))
Наносим получившийся результат на график.
abline(lmST, col = "red") abline(RlmST, col = "blue")
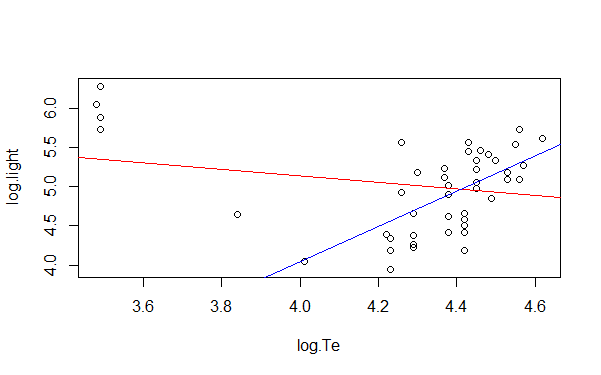
На графике мы видем красную линию, это оценка обычной линейной регрессией, а синия линия это робастная линейная регресия
Можно так же посмотреть вычесленные пораметры использовав следующие функции:
summary(RlmST) - выдаст общие данные о вычесленных регресиях, а так же оценит состав и произведет быстрый анализ вычесленной информации.
vcov(RlmST) - возвращает ковариационную матрицу основных параметров объекта подогнанной модели.
Так же можно представить разницу между обычной ленейной регрессией и робастной на данных "phones". Для этого сначала подгружаем данные.
data("phones")
Посмотрим что за данные мы хотим обработать.
summary(phones) Length Class Mode
year 24 -none- numeric calls 24 -none- numeric
Построим наши данные.
y <- phones$year c <- phones$calls plot(y,c)

Затем вычислим регресии.
m0 <- lm(c~y) abline(m0) m1 <- lmrob(c~y)
И добавляем их на график.
abline(m1) abline(m1, col ="red")
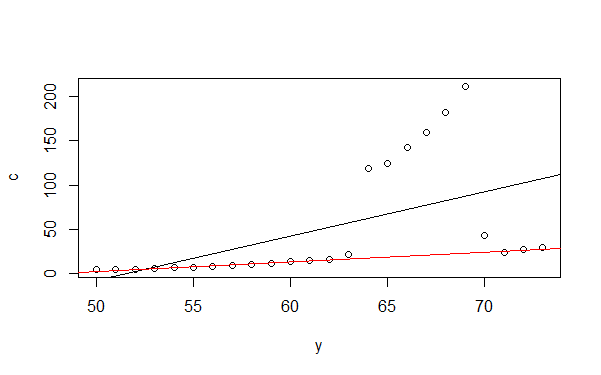
В данном случае мы видим как даёт оценку обычная линейная регрессия (чёрная) и робастная (красная).
Что следует учесть!
- Надежная регрессии не решает проблемы неоднородности дисперсии. Эта проблема может быть решена с помощью функций в sandwich - пакете после lm функции.